Skip to content

bayesian-problem-1

Problem⚑

  • 외계인의 침공에 대비하여, 지구 방위 연맹 Rarth Detense egue (EDL)은 우주 침략자를 쏘아 맞출 새로운 미사일을 개발해왔다. 물론, 몇몇 미사일은 다른 것보다 더 잘 설계되었다. 이 때 각 설계 별로 외계 우주선을 맞출 확률 x를 가정해보자.
  • 이전 실험에 따르면, 각 설계별 x의 분포는 대략 0.1과 0.4 사이에서 균등분포를 이룬다.
  • 이번에 새로운 설계안인 에일리언 블라스터 9000을 실험한다고 하자. 기사에 따르면 EDL 소장은 새 설계안으로 두 번 실험을 했고, 각 실험에서 두 번 발사했다.
  • 실험 결과는 비밀이라 소 장은 얼마나 많은 목표물을 격추했는지는 언급하지 않았으나, 기사에서 발표한 바로는 "두 번 의 실험에서 동일한 수의 목표물이 격추되었으므로, 새 설계안은 일관성이 있다"고 했다.
  • 이 데이터는 좋은가, 아니면 나쁜가? 즉, 이 데이터로 에일리언 블라스터 9000의 x에 대한 추정값이 증가하는가, 혹은 감소하는가?

Solution⚑

생각의 흐름
  • 베이즈 정리를 사용해 이 문제를 접근해보자.
  • x 에 대한 사전 분포가 주어져 있다. 이는 0.1과 0.4 사이에서 균등분포를 이룬다.
  • 이제 베이즈 정리를 통해서 어떤 사건 ( = 두 번 실험에서 동일한 수의 목표물이 격추 되었다 ) 를 관찰하였을 때, x 에 대한 믿음을 어떤 식으로 수정할 수 있을지 생각해보자.
  • 기본적으로 Bayes' theorem은 다음과 같다.
    • P(H|D) = P(D|H)P(H) / P(D)
    • 여기서 D는 데이터, H는 가설을 나타낸다.
      • D 는 "두 번 실험에서 동일한 수의 목표물이 격추 되었다" 라는 사건을 나타낸다.
      • H 는 각각의 값에 x에 대한 가설을 나타낸다.
    • 다만 P(H|D) 에서 H가 연속 변수이므로, P(H|D) 는 확률 밀도 함수로 나타낼 수 있다.
  • 그러면 P(H|D) (= 사후 분포)는 다음과 같이 계산할 수 있다.
    • P(H|D) = P(D|H)P(H) / P(D)
      • 여기서 Likelihood 는 x 가 주어졌을 때, D 가 발생할 확률을 나타낸다.
    • Bernoulli 분포를 사용하면, Likelihood 는 다음과 같이 나타낼 수 있다.
      • P(D|H) 는 두 번의 실험에서 동일한 수의 목표물이 "격추" 된 것이므로, 가능한 경우의 수는 아래와 같다.
        • A. 첫 번째 실험에서 2개의 목표물이 격추되고, 두 번째 실험에서도 2개의 목표물이 격추되는 경우
        • B. 첫 번째 실험에서 1개의 목표물이 격추되고, 두 번째 실험에서도 1개의 목표물이 격추되는 경우
        • C. 첫 번째 실험에서 0개의 목표물이 격추되고, 두 번째 실험에서도 0개의 목표물이 격추되는 경우 ( 이 경우는 격추 되지 않은 경우이므로, 이 경우는 제외한다. )
      • A. 의 경우 \(x^2 \cdot x^2 = x^4\)
      • B. 의 경우 \(2x(1-x) \cdot 2x(1-x) = 4x^2(1-x)^2\)
      • 따라서, P(D|H) = A + B = \(x^4 + 4x^2(1-x)^2\) 으로 계산할 수 있다.
    • P(H|D) = P(D|H) * P(H) / P(D) 를 이용하면
      • P(D) = ∫ P(D|H)P(H) dH = ∫ \(x^4 + 4x^2(1-x)^2\) dx = 0.0432
      • P(H|D) = \(x^4 + 4x^2(1-x)^2\)
      • P(H) = 1 / 0.3 = 10/3 ( H = 0.1 ~ 0.4 )
  • 이제 P(H|D) 를 계산하고, 이를 그래프로 나타내어 x 에 대한 추정값이 증가하는지 감소하는지 확인해보자.
    • x 에 대한 기댓값을 통해서 x 를 추정한다고 생각해보면
    • E(x) = ∫ x * P(H) dx = 0.25 ( 사전 확률 )
    • E(x) = ∫ x * P(H|D) dx = 0.29 ( 사후 확률 )
    • 사후확률이 사전확률보다 높으므로, x에 대한 추정값은 증가한다고 결론내릴 수 있겠다.

  1. 사전 분포와 데이터

    • \(x\)에 대한 사전 분포는 0.1과 0.4 사이에서 균등 분포
    • 관찰된 데이터 \(D\)는 두 번의 실험에서 동일한 수의 목표물이 격추된 것

  2. 사후 확률 계산

    • 베이즈 정리에 따라 사후 확률은

      \[ P(x|D) = \frac{P(D|x) \cdot P(x)}{P(D)} \]

    • 여기서 \(P(D|x)\) 는 주어진 \(x\)에서 데이터가 발생할 확률, \(P(x)\) 는 사전 확률, \(P(D)\)는 정규화 상수

  3. 우도 함수 \(P(D|x)\)

    • 두 번의 실험에서 동일한 수의 목표물이 격추되는 경우는

      • 경우 A: 첫 번째 실험에서 2개의 목표물이 격추되고, 두 번째 실험에서도 2개의 목표물이 격추됨.
      • 경우 B: 첫 번째 실험에서 1개의 목표물이 격추되고, 두 번째 실험에서도 1개의 목표물이 격추됨.
      • 경우 C: 첫 번째 실험에서 0개의 목표물이 격추되고, 두 번째 실험에서도 0개의 목표물이 격추됨. (이 경우는 제외)

    • 각 경우의 확률을 계산하면:

      • 경우 A: \(x^4\)
      • 경우 B: \(4x^2(1-x)^2\)

      • 따라서, 우도 함수는:

        \[ P(D|x) = x^4 + 4x^2(1-x)^2 \]

  4. 정규화 상수 \(P(D)\)

    • 정규화 상수는

      \[ P(D) = \int_{0.1}^{0.4} (x^4 + 4x^2(1-x)^2) \, dx \]

    • 계산하면 \(P(D) \approx 0.0432\) 정도 된다.

  5. 사후 확률 밀도 함수 \( P(x|D) \)

    • 사후 확률 밀도 함수는

      \[ P(x|D) = \frac{x^4 + 4x^2(1-x)^2}{0.0432} \]

  6. 기댓값 비교

    • 사전 확률의 기댓값
    \[ E(x) = \int_{0.1}^{0.4} x \cdot \frac{1}{0.3} \, dx = 0.25 \]
    • 사후 확률의 기댓값
    \[ E(x|D) = \int_{0.1}^{0.4} x \cdot P(x|D) \, dx \approx 0.29 \]

그래프⚑

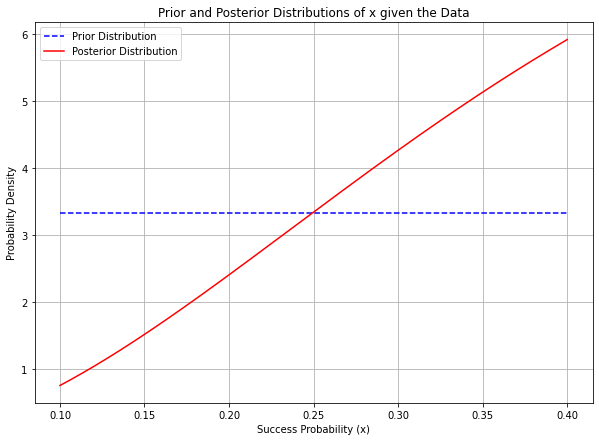
  • 사전 분포와 사후 분포를 그래프로 나타내면 다음과 같다.
  • 푸른색 균등 분포가 사전 분포이며, 빨간색이 사후 분포이다.
  • 사전에는 x 에 대한 균등 분포를 가정했으므로, 사전 분포는 상수 함수
  • "두 번 의 실험에서 동일한 수의 목표물이 격추" 라는 사실을 알게된 이후 x 에 대한 사후 분포는 선형 증가함수 모양을 띈다.
  • 이런 방식을 통해서 새롭게 알게된 사실에 대해, 우리는 체계적으로 그것에 대한 믿음을 수정할 수 있다.
파이썬 코드 
import sympy as sp
import numpy as np
import matplotlib.pyplot as plt

# 변수 정의
x = sp.Symbol('x')

# 수정된 우도 함수 정의
likelihood = 4*x**2*(1-x)**2 + x**4

# 사전 분포 정의 (균등 분포)
prior = 1 / (0.4 - 0.1)

# 증거 계산
evidence = sp.integrate(likelihood * prior, (x, 0.1, 0.4))

# 사후 분포 정의
posterior = (likelihood * prior) / evidence

# 함수로 변환
prior_func = sp.lambdify(x, prior, 'numpy')
posterior_func = sp.lambdify(x, posterior, 'numpy')

# x 값 생성
x_vals = np.linspace(0.1, 0.4, 1000)

# 사전 분포와 사후 분포 값 계산
y_prior = prior_func(x_vals)  # 이 값은 상수여야 합니다.
y_posterior = posterior_func(x_vals)

# 그래프 그리기
plt.figure(figsize=(10, 7))
plt.plot(x_vals, y_prior * np.ones_like(x_vals), label='Prior Distribution', linestyle='--', color='blue')  # 균등 분포는 상수 함수
plt.plot(x_vals, y_posterior, label='Posterior Distribution', color='red')
plt.xlabel('Success Probability (x)')
plt.ylabel('Probability Density')
plt.title('Prior and Posterior Distributions of x given the Data')
plt.legend()
plt.grid(True)
plt.show()

결론⚑

사후 확률의 기댓값이 사전 확률의 기댓값보다 크므로, 에일리언 블라스터 9000의 성공 확률 \( x \)에 대한 추정값이 증가한다고 결론지을 수 있음