multi-armed-bandit
Multi Armed Bandit (MAB) 는 피드 시스템에 적합한가?⚑
TL;DR⚑
- 게시물의 지속적으로 생성되고, 추천 아이템의 개수가 많은 피드 시스템의 경우 Multi Armed Bandit 을 통한 추천 방법론은 적합하지 않다.
- 어떤 방식이든 CVR 을 추정하기 위한 데이터가 충분히 짧은 기간 내 동기화 되지 않는다면, MAB 정책은 성공적으로 작동하지 않는다.
- 게시물의 생성 속도가 빠르다면, MAB 정책이 효과적으로 작동하지 않는다.
Thompson Sampling정책을 통해 효과적인 추천이 가능하지만, 대용량 피드 시스템에서는 계산 리소스의 이슈가 발생할 수 있어 적절하지 않다.
- Multi Armed Bandit 을 통한 추천 방법론은 소수개의 아이템 중 최적의 아이템을 추천하는 경우에 적합하다.
가정⚑
- 게시물은 각각의 고유한 전환율(CVR)을 가집니다.
- 게시물은 생성 시간을 가지며, 생성 시간 이후에만 추천될 수 있습니다.
- 추천된 게시물은 사용자에게 노출되며, 게시물의 고유한 전환율에 따라 전환이 일어납니다. ( e.g. 게시물 클릭 )
- 게시물의 최신성이나, 노출 회수에 따른 전환율의 차이는 없다고 가정합니다.
- 추천 가능한 풀을 최신 N 일 동안의 게시물로 제한하거나
- 유저에게 N 번 이상 노출된 게시물은 추천 풀에서 제거하는 등의 방법으로 이러한 가정을 근사할 수 있습니다.
측정⚑
- 각 정책의 성능을 평가하기 위해 후회(=regret)를 계산합니다.
- 시뮬레이션에서는 ( 현실 세계에서는 미리 알 수 없는 ) 각 게시물의 고유한 CVR 을 이미 알고 있다고 가정합니다.
- 게시물의 고유한 CVR 에 따라 전환되었다고 가정하고, 각 정책의 성능을 평가합니다.
- 후회는 최적 게시물을 추천했을 때의 성능과 비교하여 계산됩니다.
- 후회가 낮을수록 정책의 성능이 우수합니다.
- 실제 서비스에서는 각 게시물의 CVR 을 알 수 없기 때문에, 탐색과 착취 과정을 통해 CVR 을 추정하고, 이를 기반으로 게시물을 추천하는 방법을 사용합니다.
def measure_regret(optimal: List[Post], recommended: List[Post]):
total_optimal_cvr = sum(post.cvr for post in optimal)
total_recommended_cvr = sum(post.cvr for post in recommended)
return (total_optimal_cvr - total_recommended_cvr) / len(optimal)
코드⚑
Post ( 게시물 )⚑
Post클래스는 게시물을 나타내며, 각 게시물은 클릭률(CVR)과 생성 시간을 속성으로 가집니다.- 각
Post는 고유의 전환율을 가진다고 가정합니다. - 각 게시물은 특정 정책 하에서 몇 번 노출되었고, 몇 번의 클릭(전환)이 발생했는지를 기록합니다.
- 이 데이터는 추천 시스템이 게시물의 성능을 평가하는 데 사용됩니다.
class Post:
def __init__(self, cvr: float, created_at: int):
self.cvr = cvr
self.created_at = created_at
게시물의 생성⚑
- 각 게시물은 고유한 생성 시간과 CVR을 가집니다.
- 게시물의 CVR 의 분포는 uniform ( 균등 분포 ), 삼각 분포 ( 좌우 비대칭 ) 등 에서 샘플링되어 할당됩니다.
- 시뮬레이션은 max_time 시간 동안 진행되며, 각 t 마다 generate_rate 에 따라 새로운 게시물이 생성됩니다.
def _generate_posts(
init_size: int, max_time: int, generate_rate: float, cvr_sampling_method="uniform"
) -> List[Post]:
sampling_func = _create_sampling_func(cvr_sampling_method)
posts = [Post(cvr=sampling_func(), created_at=0) for _ in range(init_size)]
# 게시물은 generate_rate 로 속도로 유입된다.
for t in range(1, max_time + 1):
if random.random() < generate_rate:
posts.append(Post(cvr=sampling_func(), created_at=t))
return posts
Policy ( 정책 )⚑
Policy클래스는 추천 정책의 기본 틀을 제공합니다. 모든 구체적인 정책은 이 클래스를 상속받아 구현됩니다.Policy는 게시물에 대한 추천 점수 ( score ) 를 계산하는_score_post메서드와,_score_post를 바탕으로 추천할 게시물을 선택하는recommend메서드를 제공합니다.
class Policy:
def _score_post(self, post: Post) -> float:
raise NotImplementedError
def _recommend_by_score(
self, possible_candidates: List[Post], n_recommend: int
) -> List[Post]:
return sorted(possible_candidates, key=lambda post: -self._get_score(post))[
:n_recommend
]
def recommend(
self, possible_candidates: List[Post], n_recommend: int
) -> List[Post]:
return self._recommend_by_score(possible_candidates, n_recommend)
1. 무작위 추천 ( RandomPolicy )⚑
- 무작위 추천(RandomPolicy) 정책은 가능한 후보 중에서 무작위로 게시물을 추천합니다.
class RandomPolicy(Policy):
def _score_post(self, post: Post) -> float:
return random.random()
2. 최신 게시물 추천 ( NewerBetterPolicy )⚑
- 최신 게시물을 우선적으로 추천하는 정책(NewerBetterPolicy)을 구현합니다.
class NewerBetterPolicy(Policy):
def _score_post(self, post: Post) -> float:
if post.get_expose_number(self) <= self.min_expose:
return 1.0
return post.created_at
3. 엡실론 탐욕 정책 ( EpsilonGreedyPolicy )⚑
- 엡실론 탐욕 정책(EpsilonGreedyPolicy)은 무작위 추천과 탐욕 추천을 혼합한 정책입니다.
EXPLORE_POSTS_RATIO비율로 무작위 추천을 하고, 나머지 비율로 탐욕 추천을 합니다.
class EpsilonGreedyPolicy(Policy):
def _score_post(self, post) -> float:
if post.get_expose_number(self) <= self.min_expose:
return 1.0
this_score = post.get_conversion_number(self) / post.get_expose_number(self)
return this_score
def recommend(
self, possible_candidates: List[Post], n_recommend: int
) -> List[Post]:
EXPLORE_POSTS_RATIO = 0.3
# EXPLORE
random_recommend = random.sample(
possible_candidates, int(n_recommend * EXPLORE_POSTS_RATIO)
)
candidates = random_recommend
# EXPLOIT
redundant = n_recommend - int(n_recommend * EXPLORE_POSTS_RATIO)
candidates += self._recommend_by_score([p for p in possible_candidates if p not in random_recommend], redundant)
return candidates
4. 상한 신뢰구간 정책 ( UCBPolicy )⚑
- UCB 정책(UCBPolicy)은 상한 신뢰 구간(Upper Confidence Bound)을 사용하여 게시물을 추천하는 정책입니다.
class UCBPolicy(Policy):
def _score_post(self, post) -> float:
p = (post.get_conversion_number(self) + 1) / (post.get_expose_number(self) + 1)
bonus = np.sqrt(
2 * np.log(self._total_expose) / (post.get_expose_number(self) + 1)
)
return p + bonus
def recommend(
self, possible_candidates: List[Post], n_recommend: int
) -> List[Post]:
self._total_expose += n_recommend
return self._recommend_by_score(possible_candidates, n_recommend)
5. 톰슨 샘플링( ThompsonPolicy )⚑
- 톰슨 샘플링(ThompsonPolicy)은 베이지안 추론을 사용하여 게시물을 추천하는 정책입니다.
- CVR 에 대한 Posterior 분포를 추정하고, 이를 기반으로 게시물을 추천합니다.
class ThompsonPolicy(Policy):
def _score_post(self, post: Post) -> float:
return beta.rvs(
post.get_conversion_number(self) + 1,
post.get_expose_number(self) - post.get_conversion_number(self) + 1,
)
def recommend(
self, possible_candidates: List[Post], n_recommend: int
) -> List[Post]:
return self._recommend_by_score(possible_candidates, n_recommend)
데이터 동기화⚑
- 시뮬레이션에서는 매 추천마다 데이터 ( 전환횟수 / 노출 / 적합도 점수) 가 업데이트 됩니다.
- 이때 엔지니어링적인 이슈로, 특정 주기 마다 데이터가 동기화되는 것을 시뮬레이션하기 위해,
score_update_interval을 설정합니다. - 이 설정에 따라 매
score_update_interval마다 데이터가 동기화되며, 각 정책은 이를 기반으로 게시물을 CVR 을 추정하여 점수를 계산합니다. Thompson Sampling정책은 매 추천마다 모든 게시물에 대해 Scoring 이 필요하기 때문에, 모든 게시물에 대해 Scoring 이 발생합니다. 이는 상당한 계산 리소스를 필요로 합니다.
# 매 추천마다 데이터 ( 전환횟수 / 노출 / 적합도 점수) 가 업데이트 됨
if cur_time % self.config.score_update_interval == 0:
# 이벤트 큐를 시뮬레이션 합니다. ( 게시물 노출, 클릭 )
event_queue = self.get_event_queue(policy)
events = event_queue.get_event_between(
start_time=last_update + 1, end_time=cur_time
)
for _event in events:
_event.post.update_post_statistics(policy=policy)
# Thompson Sampling 은 매 추천마다 모든 게시물에 대해 Scoring 이 필요 ( beta 분포의 샘플링 )
if policy.name == "ThompsonPolicy":
for post in recommendable_posts:
policy.update_score(post=post)
# 다른 정책들은 노출이 발생한 게시물에 대해서만 Scoring 하면 충분하다
else:
for _event in events:
policy.update_score(post=_event.post)
시나리오 1 - N개의 아이템 중 최적의 아이템을 추천⚑
- N 개의 썸네일 중 최적의 썸네일을 유저에게 노출 하는 시나리오를 생각해볼 수 있습니다.
- 초기에 고정된 추천 세트가 존재하며 ( initial_size = 50 ), 중간에 게시물이 추가되지 않습니다.
-
이 상황을 시뮬레이션 하기 위해 다음과 같은 설정을 사용하여 시뮬레이션을 진행합니다.
- generate_rate = 0 ; 게시물이 추가되지 않음
- update_interval = 1 ; 매 추천마다 데이터 ( 전환횟수 / 노출 / 적합도 점수) 가 업데이트 됨
- initial_size = 50 ; 초기에 고정된 추천 세트
- max_time = 3000 ; 3000 단위 시간 동안 시뮬레이션
-
n_recommend = 5 ; 매 추천마다 5개의 게시물을 추천


예상한 바와 같이 Thompson Sampling 정책이 가장 낮은 후회를 보이며, UCB 정책이 그 다음으로 낮은 후회를 보입니다.
시나리오 2 - 피드 게시물 추천 시스템⚑
- 앞선 시나리오와 다르게, 피드 게시물 추천 시스템에서는 게시물이 지속적으로 생성됩니다.
- 또한 추천 아이템의 개수가 많아지면서, 추천 시스템의 성능을 평가하기 위한 데이터가 충분히 짧은 기간 내 동기화 되지 않습니다.
시나리오 2-1 - 게시물이 지속적으로 유입되는 경우⚑
- 이 상황을 시뮬레이션하기 위해, generate_rate = 0.1, update_interval = 1 으로 설정합니다.
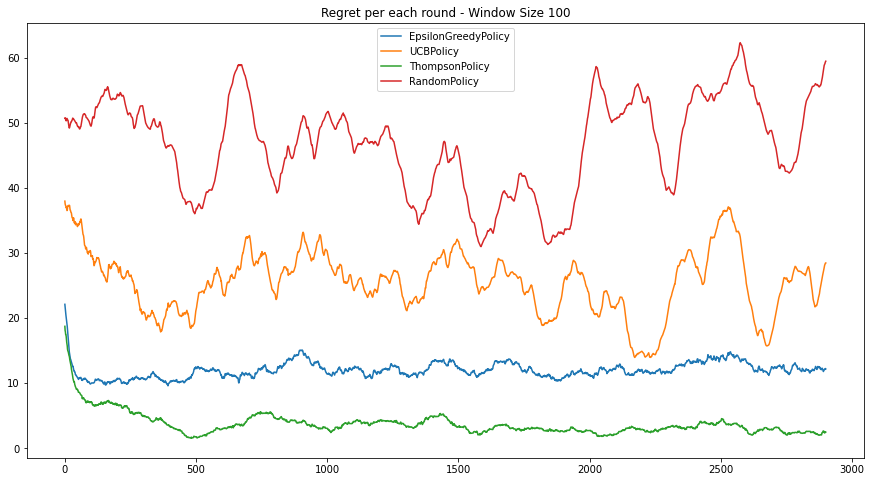

- 이 상황을 시뮬레이션하기 위해, generate_rate = 0.2, update_interval = 1 으로 설정합니다.
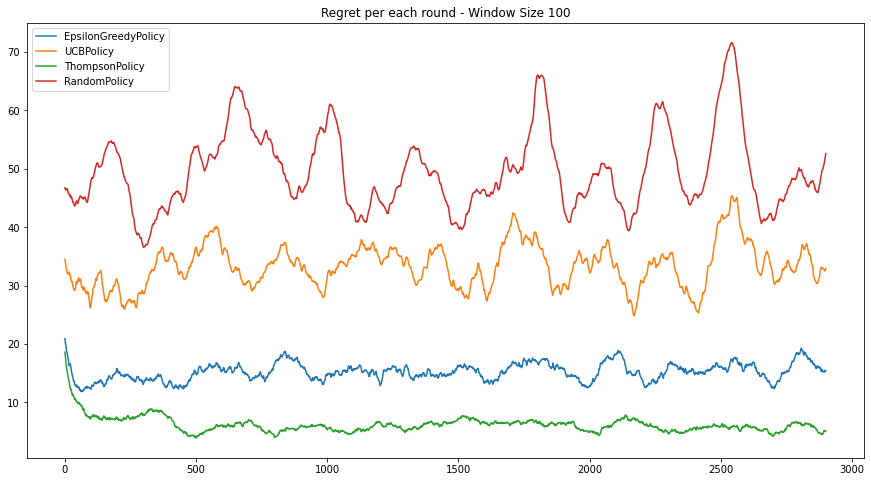

Thompson Sampling 은 여전히 좋은정책입니다. UCB는 상대적으로 수렴속도가 느려서 Epsilon Greedy 보다 낮은 성능을 보입니다.
시나리오 2-2 - 데이터 동기화 ( Post Scoring ) 에 지연이 있는 경우⚑
- 이 상황을 시뮬레이션하기 위해, generate_rate = 0.0, update_interval = 50 으로 설정합니다.


- 이 상황을 시뮬레이션하기 위해, generate_rate = 0.0, update_interval = 100 으로 설정합니다.


데이터 동기화에 지연이 일어나니 상대적으로 성능이 낮아지고 변동성 폭이 커집니다.
시나리오 2-3 - 데이터 동기화가의 지연이 있으며, 동시에 게시물이 지속적으로 유입되는 경우⚑
- 이 상황을 시뮬레이션하기 위해, generate_rate = 0.1, update_interval = 50 으로 설정합니다.
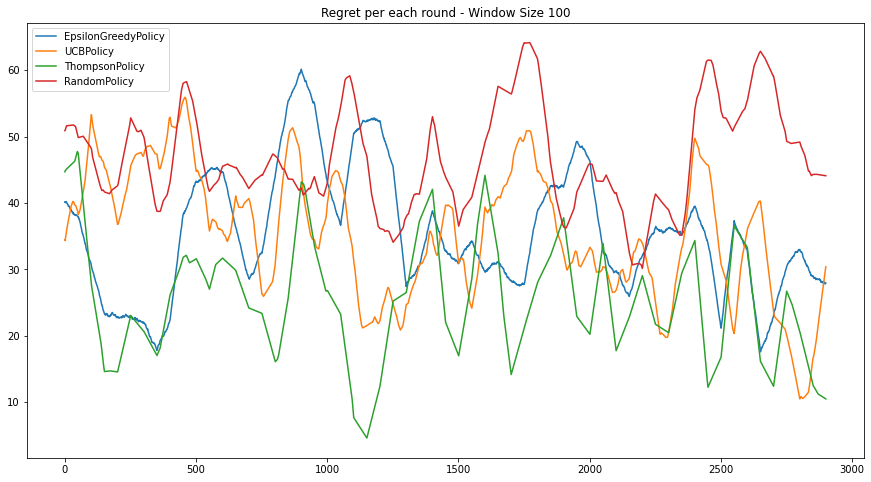

- 이 상황을 시뮬레이션하기 위해, generate_rate = 0.2, update_interval = 100 으로 설정합니다.

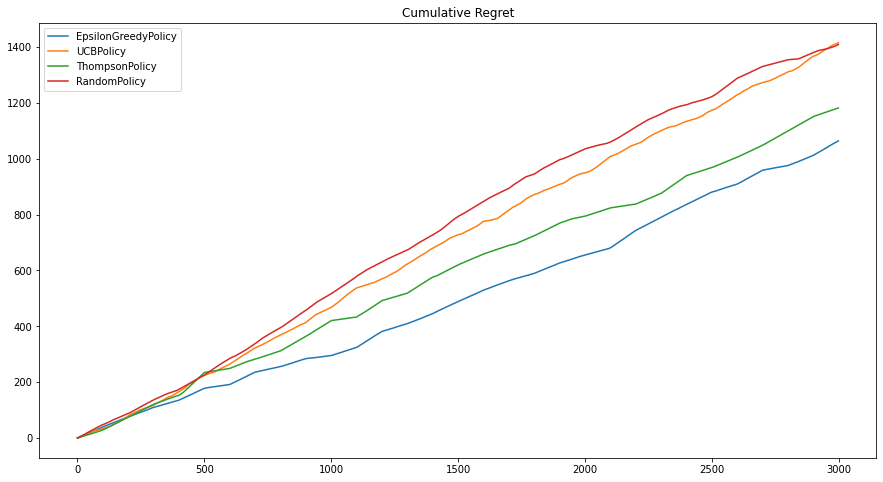
데이터의 동기화 지연과 게시물이 지속적으로 유입되는 경우, 각 정책의 성능은 급격하게 나빠지기 시작합니다.
결론⚑
- 일반적으로 multi-armed bandit 을 통한 추천 방법론은 소수개의 아이템 중 최적의 아이템을 추천하는 경우에 적합합니다.
- 게시물의 지속적으로 생성되고, 추천 아이템의 개수가 많은 피드 시스템의 경우 Multi Armed Bandit 을 통한 추천 방법론은 적합하지 않습니다.
- 물론
Thompson Sampling방법론은 효과적인 추천이 가능합니다. - 그러나 그것을 위해서는 Update interval 이 짧아야 하며, 추천 가능한 모든 대상에 대해서 Scoring 이 매 추천마다 발생해야 합니다.
- 따라서 대용량 피드 시스템에서는 계산 리소스의 이슈가 발생할 수 있고, 이는 효과적인 추천 알고리즘이 아닙니다.
- 물론
Full Implementation⚑
import random
from collections import defaultdict
from dataclasses import dataclass
from enum import Enum
from typing import Callable, List
from uuid import uuid4
import matplotlib.pyplot as plt
import numpy as np
from scipy.stats import bernoulli, beta, triang, uniform
class Post:
def __init__(self, cvr: float, created_at: int):
self.id = uuid4()
self.cvr = cvr
self.created_at = created_at
self._expose_cnt = defaultdict(lambda: 0)
self._conversion_cnt = defaultdict(lambda: 0)
def __hash__(self):
return hash(self.id)
def __eq__(self, other):
if isinstance(other, Post):
if self.id == other.id:
return True
return False
def __str__(self):
output = ""
for k in self._expose_cnt:
output += f"{k} - {self._conversion_cnt[k]} / {self._expose_cnt[k]} \n"
output += f"cvr : {self.cvr} / created_at = {self.created_at}"
return output
def update_post_statistics(self, policy: "Policy"):
self._expose_cnt[policy] += 1
self._conversion_cnt[policy] += bernoulli.rvs(self.cvr)
def get_expose_number(self, policy: "Policy"):
return self._expose_cnt[policy]
def get_conversion_number(self, policy: "Policy"):
return self._conversion_cnt[policy]
def _create_sampling_func(method: str) -> Callable:
if method == "uniform":
sampling_func = uniform.rvs
elif method == "left":
c = 0
sampling_func = lambda: triang.rvs(c)
elif method == "right":
c = 1
sampling_func = lambda: triang.rvs(c)
return sampling_func
def measure_regret(optimal: List[Post], recommended: List[Post]):
assert len(optimal) == len(recommended), "length of two lists must be same"
total_optimal_cvr = sum(post.cvr for post in optimal)
total_recommended_cvr = sum(post.cvr for post in recommended)
return (total_optimal_cvr - total_recommended_cvr) / len(optimal)
class Policy:
def __init__(self, config: "Config"):
self.min_expose = config.min_expose
self._cache = {}
self._total_expose = 0
@property
def name(self) -> str:
return self.__class__.__name__
def __eq__(self, other):
if self.name == other.name:
return True
return False
def __hash__(self):
return hash(self.name)
def __str__(self):
return self.name
def _score_post(self, post: Post) -> float:
raise NotImplementedError
def _get_score(self, post: Post) -> float:
if self._cache.get(post) is not None:
return self._cache.get(post)
self._cache[post] = self._score_post(post)
return self._cache[post]
def _recommend_by_score(
self, possible_candidates: List[Post], n_recommend: int
) -> List[Post]:
return sorted(possible_candidates, key=lambda post: -self._get_score(post))[
:n_recommend
]
def recommend(
self, possible_candidates: List[Post], n_recommend: int
) -> List[Post]:
def update_score(self, post: Post):
self._cache[post] = self._score_post(post)
class RandomPolicy(Policy):
def _score_post(self, post: Post) -> float:
return random.random()
def recommend(
self, possible_candidates: List[Post], n_recommend: int
) -> List[Post]:
return self._recommend_by_score(possible_candidates, n_recommend)
class NewerBetterPolicy(Policy):
def _score_post(self, post: Post) -> float:
if post.get_expose_number(self) <= self.min_expose:
return 1.0
return post.created_at
def recommend(
self, possible_candidates: List[Post], n_recommend: int
) -> List[Post]:
return self._recommend_by_score(possible_candidates, n_recommend)
class EpsilonGreedyPolicy(Policy):
def _score_post(self, post) -> float:
if post.get_expose_number(self) <= self.min_expose:
return 1.0
this_score = post.get_conversion_number(self) / post.get_expose_number(self)
return this_score
def recommend(
self, possible_candidates: List[Post], n_recommend: int
) -> List[Post]:
EXPLORE_POSTS_RATIO = 0.3
# EXPLORE
random_recommend = random.sample(
possible_candidates, int(n_recommend * EXPLORE_POSTS_RATIO)
)
candidates = random_recommend
# EXPLOIT
redundant = n_recommend - int(n_recommend * EXPLORE_POSTS_RATIO)
candidates += self._recommend_by_score(
[p for p in possible_candidates if p not in random_recommend], redundant
)
return candidates
class UCBPolicy(Policy):
def _score_post(self, post) -> float:
p = (post.get_conversion_number(self) + 1) / (post.get_expose_number(self) + 1)
bonus = np.sqrt(
2 * np.log(self._total_expose + 1) / (post.get_expose_number(self) + 1)
)
return p + bonus
def recommend(
self, possible_candidates: List[Post], n_recommend: int
) -> List[Post]:
self._total_expose += n_recommend
return self._recommend_by_score(possible_candidates, n_recommend)
class ThompsonPolicy(Policy):
def _score_post(self, post: Post) -> float:
return beta.rvs(
post.get_conversion_number(self) + 1,
post.get_expose_number(self) - post.get_conversion_number(self) + 1,
)
def recommend(
self, possible_candidates: List[Post], n_recommend: int
) -> List[Post]:
return self._recommend_by_score(possible_candidates, n_recommend)
class EventType(Enum):
EXPOSED = "exposed"
class Event:
def __init__(self, time: int, post: Post, event_type: EventType):
self.time = time
self.post = post
self.event_type = event_type
class EventQueue:
def __init__(self):
self.queue: List[Event] = []
def push(self, event: Event):
self.queue.append(event)
def get_event_between(self, start_time: int, end_time: int) -> List[Event]:
return [event for event in self.queue if start_time <= event.time <= end_time]
@dataclass
class Config:
# post generation
init_size: int
max_time: int
gen_rate: float
cvr_sampling_method: str
# policy
min_expose: int
n_recommend: int
score_update_interval: int
def _generate_posts(
init_size=100, max_time=1000, generate_rate=0.01, cvr_sampling_method="uniform"
) -> List[Post]:
sampling_func = _create_sampling_func(cvr_sampling_method)
posts = [Post(cvr=sampling_func(), created_at=0) for _ in range(init_size)]
for t in range(1, max_time + 1):
if random.random() < generate_rate:
posts.append(Post(cvr=sampling_func(), created_at=t))
return posts
class Experiment:
def __init__(self, config: Config):
self.config = config
self.event_queues = defaultdict(EventQueue)
self.regret_log = defaultdict(list)
self._prepare()
def _prepare(self):
self.generated_posts = _generate_posts(
init_size=self.config.init_size,
max_time=self.config.max_time,
generate_rate=self.config.gen_rate,
cvr_sampling_method=self.config.cvr_sampling_method,
)
def _log_regret(self, policy: Policy, regret: float) -> None:
self.regret_log[policy].append(regret)
def get_event_queue(self, policy: Policy):
return self.event_queues[policy]
def play_scenario(self, policy: Policy) -> None:
last_update = -1
for cur_time in range(self.config.max_time):
# filter recommendable posts
recommendable_posts = list(
filter(lambda p: p.created_at <= cur_time, self.generated_posts)
)
# optimal recommendation
optimal_recommendation = sorted(recommendable_posts, key=lambda p: -p.cvr)[
: self.config.n_recommend
]
# actual recommendation
actual_recommendation = policy.recommend(
possible_candidates=recommendable_posts,
n_recommend=self.config.n_recommend,
)
# publish event
for post in actual_recommendation:
self.get_event_queue(policy).push(
Event(time=cur_time, post=post, event_type=EventType.EXPOSED)
)
# measure regret
regret = measure_regret(optimal_recommendation, actual_recommendation)
self._log_regret(policy, regret)
# update data
if cur_time % self.config.score_update_interval == 0:
event_queue = self.get_event_queue(policy)
events = event_queue.get_event_between(
start_time=last_update + 1, end_time=cur_time
)
for _event in events:
_event.post.update_post_statistics(policy=policy)
if policy.name == "ThompsonPolicy":
for post in recommendable_posts:
policy.update_score(post=post)
else:
for _event in events:
policy.update_score(post=_event.post)
last_update = cur_time
def plot_regret(self, policy: Policy, window_size=10):
def moving_average(x, w):
return np.convolve(x, np.ones(w), "valid")
smoothed_regret = moving_average(np.array(self.regret_log[policy]), window_size)
plt.title(f"Regret per each round - Window Size {window_size}")
plt.plot(smoothed_regret, label=policy)
def plot_cum_regret(self, policy: Policy):
plt.title("Cumulative Regret")
plt.plot(np.cumsum(self.regret_log[policy]), label=policy)
config = Config(
init_size=50,
max_time=3000,
gen_rate=0.05,
cvr_sampling_method="uniform",
score_update_interval=100,
n_recommend=5,
min_expose=1,
)
experiment = Experiment(config=config)
policies = [
EpsilonGreedyPolicy(config),
UCBPolicy(config),
ThompsonPolicy(config),
RandomPolicy(config),
# NewerBetterPolicy(config),
]
for policy in policies:
experiment.play_scenario(policy)
# REGRET PLOT
plt.figure(figsize=(15, 8))
for policy in policies:
experiment.plot_regret(policy=policy, window_size=100)
print(f"{policy.name} : avg_regret = {np.mean(experiment.regret_log[policy])}")
plt.legend()
plt.figure(figsize=(15, 8))
for policy in policies:
experiment.plot_cum_regret(policy=policy)
plt.legend()