carrying-capacity
TL;DR⚑
- 토스 리더가 말하는 Carrying Capacity(CC) 개념은 제품의 본질적인 성장 한계를 낸다.
- 신규 유저 유입(Inflow)과 이탈률(Churn)를 통해서 CC를 계산할 수 있다.
- CC를 이해하고 개선하는 것이 제품 성장의 핵심
Carrying Capacity ( =CC ) 란?⚑
- CC는 서비스가 도달할 수 있는 최종적인 유저 수를 의미함.
- CC = 매일 새로 오는 유저 수 / 매일 잃게 되는 유저의 비율로 계산됨.
- 제품의 본질적인 체력을 나타내는 지표임.
CC 개념을 통해 해결할 수 있는 질문⚑
- 특정 행동을 모든 유저에게 강요하는 것이 도움이 될까?
- 24시간 서비스 장애가 장기적으로 악영향을 줄까?
- 하루 10만 명의 유저 방문과 매주 70만 명의 유저 방문은 같은 의미일까?
- 광고를 계속 틀면 유저가 계속 늘어날까?
- 서비스 알림 시스템 문제로 유저가 감소했다면, 이는 큰 문제일까?
- 위 질문에 답할 수 있는 핵심 개념이 바로 Carrying Capacity(CC)임.
CC의 특징⚑
- 대부분의 경우, 신규 유저 유입 수는 일정한 상수로 유지됨.
- 이탈률도 대체로 일정하게 유지되는 경향이 있음.
- CC는 보통 서비스 런칭 후 3-6개월 내에 계산 가능함.
Inflow (유입)⚑
- New (Organic): 자연적으로 유입되는 신규 유저
- Resurrection: 다시 돌아온 유저
- Paid: 광고를 통해 유입된 유저
- Viral: 바이럴 효과로 유입된 유저
Churn (이탈)⚑
- 전체 유저 중 서비스를 떠나는 비율
- 보통 3개월 이상 서비스를 사용하지 않는 유저를 이탈로 정의함.
CC의 계산⚑
-
CC =
# of New Daily Customers/% Customers You Lost Each Day# of New Daily Customers는 적당한 Time window 로 설정하는데 보통 Weekly 로
\[\frac{dN}{dt} = i - rN = 0\] -
CC는 유입과 관련한 미분방정식의 Steady State 를 계산하는 것이라 생각하면 됨
- 아래 식에서 i는 유입, r은 이탈률, N은 유저 수를 의미
- 위 특징에서 언급하듯 이승건 대표는 i와 r 을 상수로 가정하고 계산
- \(\frac{dN}{dt} = 0\) 인 상태에서의 평형 유저숫자 \(N^{*}\) 를 찾는 것이 CC 계산임
- \(i^{*}= rN^{*}\) 이므로 \(N^{*} = \frac{i}{r}\) 으로 도출 할 수 있고, 이것이 CC 를 계산하는 방법임
Example⚑
- 미분방정식의 해를 도출함으로써, CC 를 계산할 수 있음
- 아래 그림의 예시처럼 마케팅 끄면 다시 돌아오는 것을 확인할 수 있음
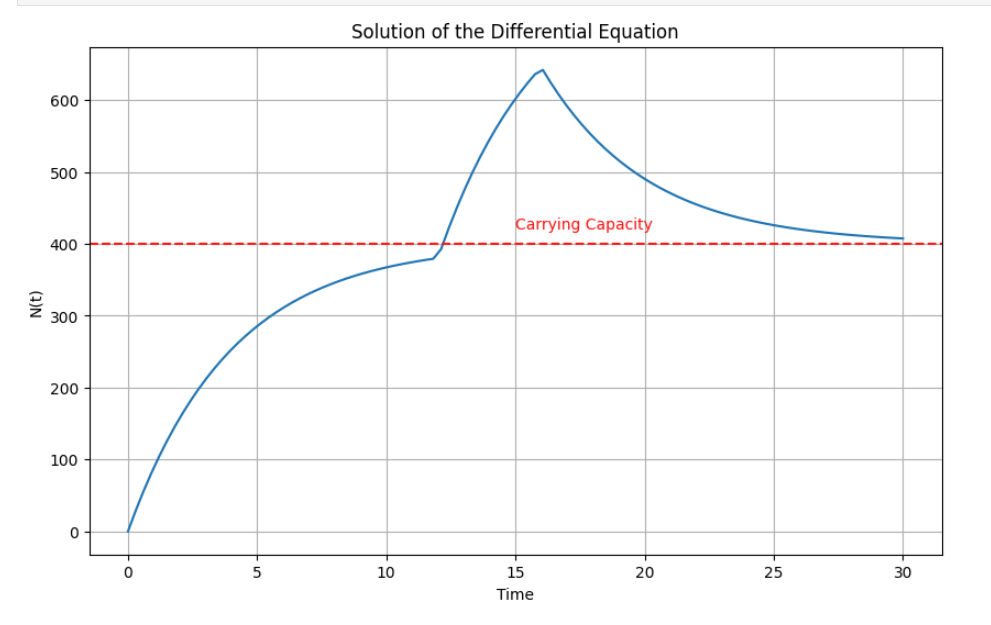
파이썬 코드
- 아래 파이썬 코드를 통해서, 유입과 이탈률이 상수로 가정되었을 때, N의 추세를 생각해볼 수 있음
import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt
organic_influx = 100
marketing_influx = 100
churn_rate = 0.25
carrying_capacity = organic_influx / churn_rate
def i(t):
if 0 < t <= 12:
return organic_influx
elif 12 < t <= 16:
return organic_influx + marketing_influx
else:
return organic_influx
def r(t):
return churn_rate
def dN_dt(N, t):
return i(t) - r(t) * N
# Initial condition and time range
N0 = 0
t = np.linspace(0, 30, 100)
# Solve the differential equation
N = odeint(dN_dt, N0, t)
# Plot the solution
plt.figure(figsize=(10, 6))
plt.plot(t, N)
plt.xlabel('Time')
plt.ylabel('N(t)')
plt.title('Solution of the Differential Equation')
plt.axhline(y=carrying_capacity, color='r', linestyle='--', label='Carrying Capacity')
plt.text(15, carrying_capacity + 20, 'Carrying Capacity', color='r')
plt.grid(True)
plt.show()
CC 개선 전략⚑
- AARRR 퍼널의 역순으로 개선해야 함: Retention → Activation → Acquisition
- 리텐션 개선이 가장 중요하며, 이는 제품의 본질적인 가치를 높이는 것을 의미함.
- 광고나 마케팅은 단기적으로 유저 수를 늘릴 수 있지만, CC 자체를 개선하지는 못함.
- 린 스타트업에서 리텐션을 필두로하는 성장가설 검증에 힘쓰는 이유가 여기에 있음.

- 곰곰이 생각해보면, CC 를 정의하는 미분방정식에서 상수항은 큰 의미가 없음, 중요한 것은 N에 대한 비율로서 작동하는 것이 CC 에 영향을 미침
- 따라서 현재 유저수에 비례하는 리텐션 개선이 CC 개선에 가장 큰 영향을 미침
CC 개념을 통해 해결할 수 있는 질문 - 정답⚑
- 특정 행동을 모든 유저에게 강요하는 것이 도움이 될까?
- 단순히 상관관계를 인과관계로 해석하면 안됨
- 모름, 결국 r (리텐션) 에 영향을 미치는지 여부 확인해봐야 함
- 24시간 서비스 장애가 장기적으로 악영향을 줄까?
- i (유입) 와 r (리텐션) 에 영향 주는 것 보면 됨
- 보통 단기 장에는 둘에 영향을 잘 미치지 않아서, MAU 에 영향 크게 안줌
- 하루 10만 명의 유저 방문과 매주 70만 명의 유저 방문은 같은 의미일까?
- 광고를 계속 틀면 유저가 계속 늘어날까?
- 광고는 일시적으로 i 에 영향을 줄 수 있음
- 그러나 광고 끄면 다시 CC 로 수렴해갈 것 ( 위 그림 참조 )
- 서비스 알림 시스템 문제로 유저가 감소했다면, 이는 큰 문제일까?
- 들어오는 유저수 말고 나가는 유저도 변하는지 봐야 함
결론⚑
- CC는 제품의 근본적인 성장 잠재력을 나타내는 지표임.
- PO는 CC를 이해하고 개선하는 데 집중해야 하며, 이는 주로 제품의 본질적인 가치를 높이고 리텐션을 개선하는 것으로 달성할 수 있음.
- 단기적인 성과에 집중하기보다는 장기적인 관점에서 CC를 높이는 전략이 중요함.