alpha-geometry
Alpha geometry⚑
Problem⚑
- 현재의 기계 학습 접근 방식은 인간의 증명을 기계 검증 형식으로 번역하는 데 높은 비용이 들기 때문에 대부분의 수학적 영역에 적용할 수 없음.
- 특히 기하학은 고유한 번역 (= 사람의 풀이를 기계가 검증할 수 있는 형태로의 변환 ) 문제 로 인해 이 문제가 더욱 심각하며, 그로 인해 훈련 데이터가 매우 부족함
Contribution⚑
- AlphaGeometry는 인간의 시범을 필요로 하지 않음
- 다양한 복잡성 수준에서 수백만 개의 정리와 증명을 합성
- 기하학 문제를 Deduction Database 과 Algebraic Reasoning 을 사용하여 생성한 데이터 셋을 학습 시키고, 이를 이용하여 기하학 문제를 풀어내는 방법을 제안
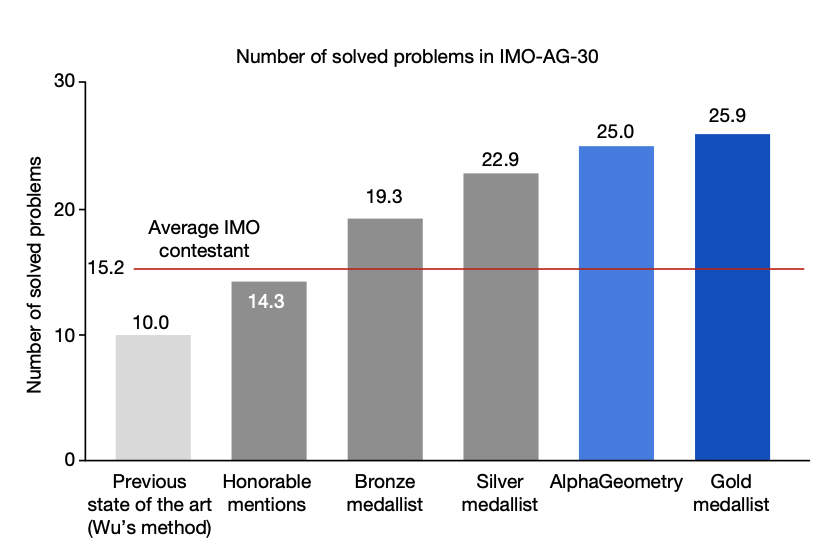
- 최신 올림피아드 수준의 문제 30개로 구성된 테스트 세트에서 AlphaGeometry는 25개의 문제를 해결하여 10개의 문제만 해결하는 이전 최고의 방법을 능가하며 평균 국제 수학 올림피아드 (IMO) 금메달리스트의 성과에 접근했음
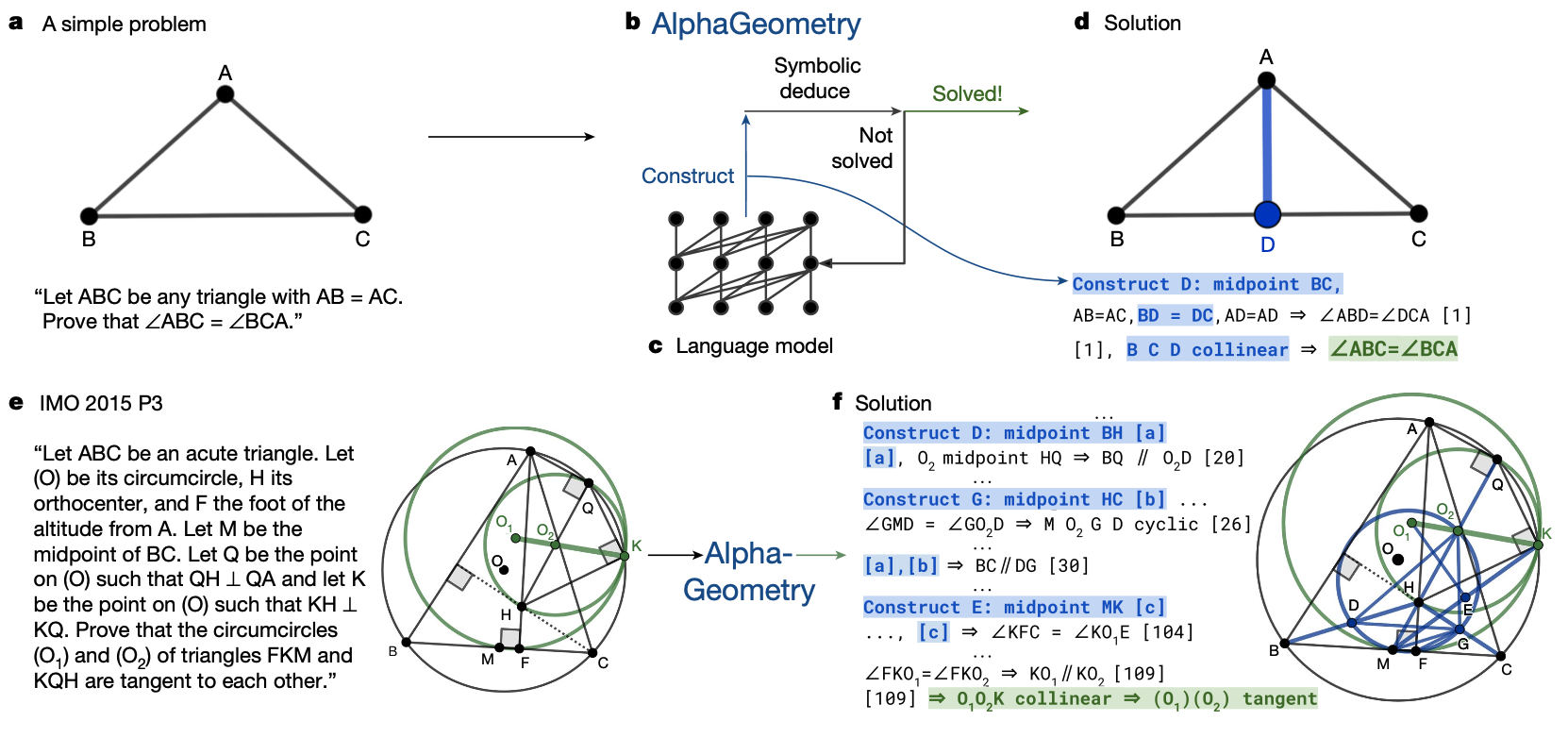
Solving Strategy⚑
- 그림은 AlphaGeometry의 개요와 간단한 문제와 IMO 2015 문제 3을 해결하는 방법을 보여준다.
- 문제가 주어진다
- Symbolic Deduce 를 적용한다
- Solve 되었는지 확인한다
- Solve 되지 않은 경우 Language Model 을 사용하여 보조 점을 구성한다.
- 다시 Symbolic Deduce 를 적용한다.
- 문제가 해결될 때까지 4, 5를 반복한다.
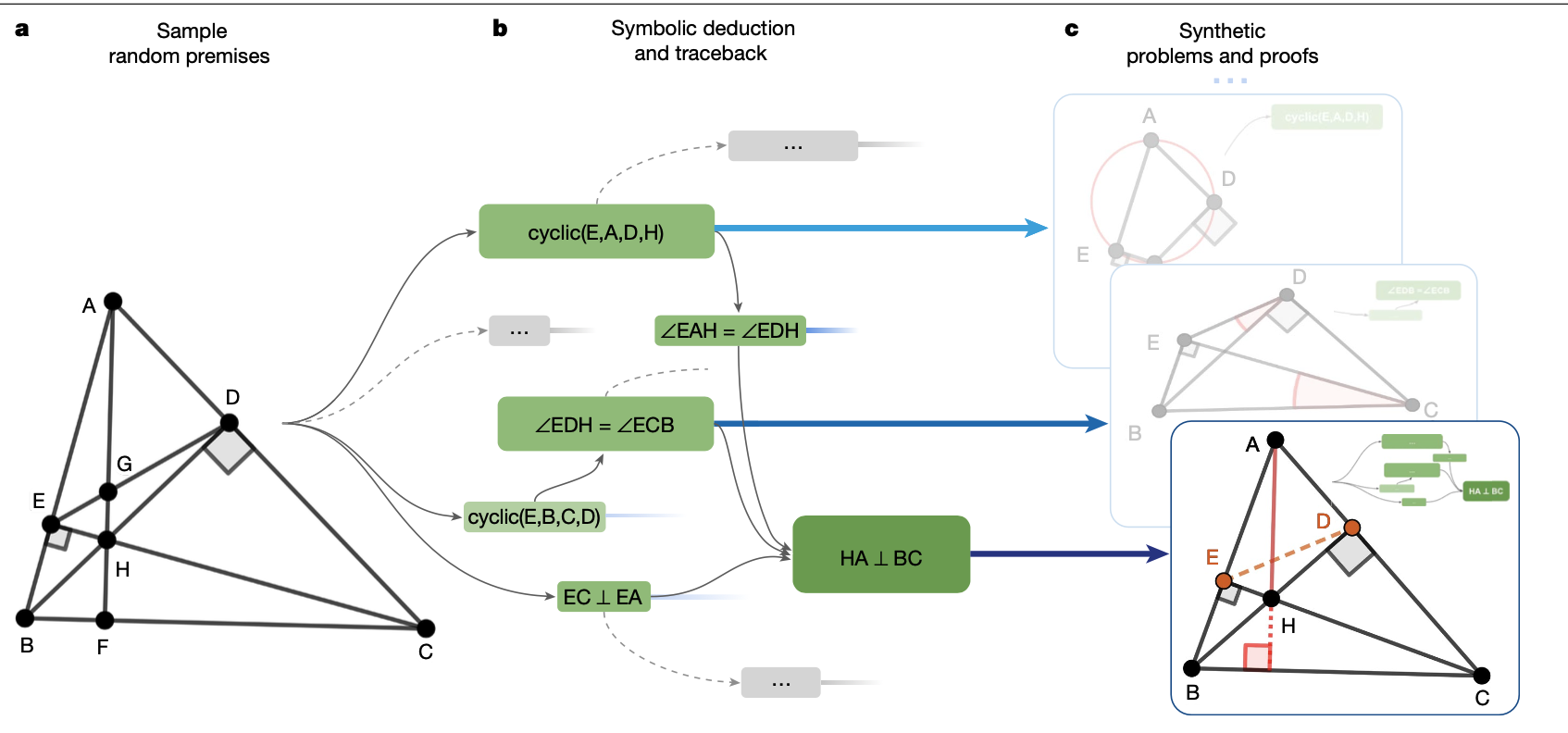
Data Generation⚑
-
합성 데이터 생성 방법
- 합성 데이터 생성 과정은 무작위로 정리 전제 (Premise) 를 샘플링하여 상징적 추론 엔진 (Symbolic Deduction Engine) 에 입력하는 것에서 시작했음.
- 샘플링된 전제는 전방 추론 규칙을 사용하여 새로운 참 진술을 연역하며, 결과는 방향성 비순환 그래프로 반환됨.
- 방향성 비순환 그래프의 노드들은 도달 가능한 결론을 나타내며, 이로부터 합성 훈련 예제 (전제, 결론, 증명)을 생성했음.
-
기하학적 합성 데이터 생성
- 기하학에서는 상징적 추론 엔진이 기하학적 규칙을 통해 전제로부터 새로운 진술을 연역하는 역할을 함.
- 연역 규칙은 확정형 호른 절의 형태로, 점 객체에 대한 기하학적 술어를 포함하고 있음.
- 대수적 규칙(AR)을 도입하여 각도, 비율, 거리 추적이 가능한 추가적인 기하학적 연역을 수행함.
- DD와 AR의 를 재귀적으로 수행하여 비순환 방향그래프를 통한 증명을 생성하고, 이를 통해 합성 훈련세트 (전제, 결론, 증명) = (P, N, G(N))을 얻었음
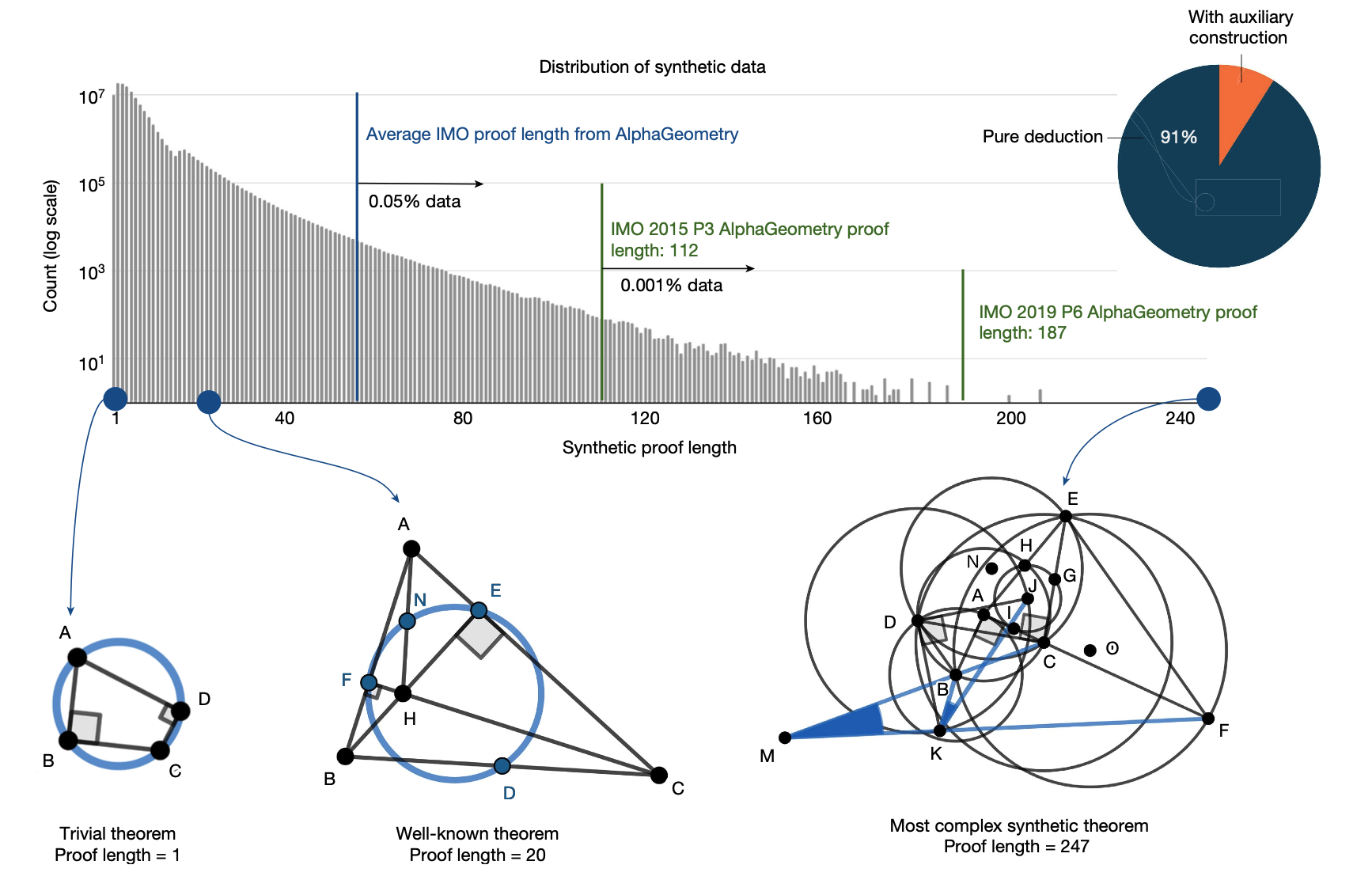
- 합성 데이터의 결과와 발견
- 합성 데이터 생성 과정에서 기하학 문헌에 알려진 복잡한 정리와 보조정리를 재발견할 수 있었음.
- 합성 증명의 길이는 짧은 쪽으로 치우쳐 있지만, 일부는 IMO 테스트 세트의 가장 어려운 문제보다 30% 더 긴 증명을 포함하고 있음.
- 합성 정리는 인간의 미적 편견에 구속되지 않으며, 유클리드 기하학의 더 넓은 시나리오 집합을 다루고 있음.
- 중복 제거 후, 1억 개 이상의 고유한 정리와 증명을 얻었으며, 이 과정에서 IMO-AG-30 ( 테스트에 사용 ) 정리는 발견되지 않았음.
Deduction Database (DD)⚑
- Deduction Database(DD)는 기하학적 정리와 증명을 연역하기 위한 규칙들을 포함한 데이터베이스임.
- DD는 기하학적 술어와 그 관계를 나타내며, 전제와 결론을 형식적으로 표현해 증명 과정을 구성함.
- DD에서 사용되는 기하학적 술어에는 점이 동일한 선상에 있는지, 평행한지, 수직인지를 나타내는 술어들이 있음.
- 이러한 기하학적 술어와 연역 규칙을 조합하여 문제를 풀 수 있음.
Toy Example for Explanation
Example Deduction Engine⚑
- http://www.mmrc.iss.ac.cn/~xgao/paper/jar-gdbase.pdf
-
predicates로 다음과 같은 것들이 소개된다- points (A, B, C) - 세 점 A, B, C 가 존재한다.
- coll (E, A, C) - 점 E, A, C 가 같은 선상에 존재한다.
- para (A, B, C, D) - AB 와 CD 가 평행하다.
- perp (A, B, C, D) - AB 와 CD 가 수직이다.
- midp (M, A, B) - M 은 A와 B의 중점이다.
-
premise는 전제를 의미한다. 문제에서 주어진 조건들을 형식적으로 변환한 것을 의미한다.- 다음과 같은 예시를 생각해볼 수 있다.
premises = [ ("triangle", "A", "B", "C"), ("interior_angle", "angle_ABC", "C") ]triangle은 세 점이 삼각형을 이룬다는 것을 의미한다.interior_angle은 내각을 의미한다. ABC 의 내각이 C 라는 것을 의미한다.
-
conclusion은 결론을 의미한다. 문제에서 구해야 하는 것을 형식적으로 표현한 것을 의미한다.- 다음과 같은 예시를 생각해볼 수 있다.
goal = ("exterior_angle", "angle_ABC", "angle_BCA", "angle_CAB")exterior_angle은 외각을 의미한다. ABC 의 외각이 BCA 와 CAB 의 합이라는 것을 의미한다.
-
deduction rule은 추론 규칙을 의미한다.- 전제로부터 결론을 도출하는 방법을 의미한다.
- 아래와 같이, 어떤 전제가 주어질 때 도출할 수 있는 연역적 규칙들을 의미한다.
- Modus_ponens 와 같은 추론 규칙을 생각해볼 수 있다.
def exterior_angle_of_triangle(premises): new_conclusions = [] for premise1 in premises: if premise1[0] == "triangle": A, B, C = premise1[1], premise1[2], premise1[3] # 추가적인 전제를 검사합니다. for premise2 in premises: if premise2[0] == "interior_angle": interior_angle, vertex = premise2[1], premise2[2] if vertex == C and interior_angle == f"angle_{A}{B}{C}": new_conclusions.append( ( "exterior_angle", f"angle_{B}{A}{C}", f"angle_{A}{B}{C}", f"angle_{B}{C}{A}", ) ) return new_conclusions -
solver는 주어진premises와deduction rule을 반복적으로 적용하여goal을 도출하는 과정을 의미# Solver def apply_deduction_rules(premises, goal=None, max_iterations=10000): conclusions = [] seen_premises = set(premises) iterations = 0 while True: new_conclusions = [] iterations += 1 # Apply each deduction strategy for strategy in [ sum_of_angles_in_triangle, exterior_angle_of_triangle, ]: strategy_conclusions = strategy(premises) for conclusion in strategy_conclusions: if conclusion not in seen_premises: new_conclusions.append(conclusion) seen_premises.add(conclusion) # Check if the goal has been achieved if goal and conclusion == goal: conclusions.append(conclusion) return conclusions # If no new conclusions, break the loop if not new_conclusions: break # If maximum iterations reached, break the loop if iterations >= max_iterations: print("Max iterations reached, stopping deduction") break conclusions.extend(new_conclusions) premises.extend(new_conclusions) # Update premises with new conclusions return conclusions def traceback(conclusions, premises): proof = premises.copy() for conclusion in conclusions: if conclusion not in proof: proof.append(conclusion) return proof -
종합적으로 Deduction Engine 을 이용해 문제를 푸는 과정은 다음과 같이 생각해볼 수 있다.
# 예시: 다양한 전제와 추론 규칙 적용 premises = [ ("triangle", "A", "B", "C"), ("interior_angle", "angle_ABC", "C") # 내각의 전제를 추가합니다. ] goal = ("exterior_angle", "angle_ABC", "angle_BCA", "angle_CAB") conclusions = apply_deduction_rules(premises, goal) proof = traceback(conclusions, premises) print(f"Proof:") for step in proof: print(step)
Example
- M 이 AB 의 중점이고, O 가 AB 에 수직이라면, OA 와 OB 는 같다는 것을 도출하는 deduction rule 을 도출하는 코드이다.
- 해당 코드는 여기 에서 확인할 수 있다.
def match_midp_perp_cong(
g: gh.Graph,
g_matcher: Callable[str, list[tuple[gm.Point, ...]]],
theorem: pr.Theorem,
) -> Generator[dict[str, gm.Point], None, None]:
"""Match midp M A B, perp O M A B => cong O A O B."""
for m, a, b in g.all_midps():
ab = g._get_line(a, b)
for l in m.neighbors(gm.Line):
if g.check_perpl(l, ab):
for o in l.neighbors(gm.Point):
if o != m:
yield dict(zip('ABMO', [a, b, m, o]))
Algebraic Reasoning Engine ( AR )⚑
- Algebraic Reasoning Engine(AR)은 대수적 관계와 기하학적 상수를 처리해 기하학 문제를 해결하는 역할을 함.
- 기하학에서의 대수적 연역을 수행하기 위해 Gaussian 소거법을 사용함.
- 기하학적 상수나 거리, 각도와 같은 대수적 관계를 처리하여 새로운 결론을 도출할 수 있음.
- AR은 복잡한 대수적 조작과 연역을 다룰 수 있어, 기존의 기하학적 증명 방법을 확장함.
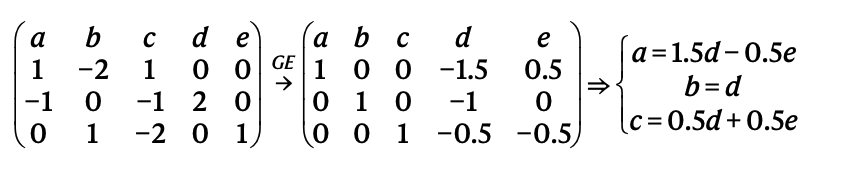
Example
class GeometricTable(Table):
"""Abstract class representing the coefficient matrix (table) A."""
# ... 생략
def get_all_eqs_and_why(
self, return_quads: bool
) -> Generator[Any, None, None]:
for out in super().get_all_eqs_and_why(return_quads):
if len(out) == 3:
x, y, why = out
x, y = self.map2obj([x, y])
yield x, y, why
if len(out) == 4:
x, y, f, why = out
x, y = self.map2obj([x, y])
yield x, y, f, why
if len(out) == 5:
a, b, x, y, why = out
a, b, x, y = self.map2obj([a, b, x, y])
yield a, b, x, y, why
- 아래 예시를 보면
add_eq,add_const_ratio,add_eqratio를 통해서 전제를 추가하고,get_all_eqs_and_why를 통해 새롭게 결론을 도출하는 AR 과정을 확인할 수 있다. - 실제 코드 예시는 여기 있다.
class RatioTable(GeometricTable):
"""Coefficient matrix A for log(distance)."""
def __init__(self, name: str = ''):
name = name or '1'
super().__init__(name)
self.one = self.const
def add_eq(self, l1: gm.Length, l2: gm.Length, dep: pr.Dependency) -> None:
l1, l2 = self.get_name([l1, l2])
return super().add_eq3(l1, l2, 0.0, dep)
def add_const_ratio(
self, l1: gm.Length, l2: gm.Length, m: float, n: float, dep: pr.Dependency
) -> None:
l1, l2 = self.get_name([l1, l2])
return super().add_eq2(l1, l2, m, n, dep)
def add_eqratio(
self,
l1: gm.Length,
l2: gm.Length,
l3: gm.Length,
l4: gm.Length,
dep: pr.Dependency,
) -> None:
l1, l2, l3, l4 = self.get_name([l1, l2, l3, l4])
return self.add_eq4(l1, l2, l3, l4, dep)
def get_all_eqs_and_why(self) -> Generator[Any, None, None]:
return super().get_all_eqs_and_why(True)
- 실제로 AR 이 적용되는 코드는 여기 에서 확인할 수 있다.
Training LM⚑
- Transformer 언어 모델은 텍스트 시퀀스를 생성하는 강력한 딥러닝 모델
- (P, N, G(N))을 '<전제> <결론> <증명>' 구조의 텍스트 문자열로 직렬화하여 언어 모델을 훈련시켰음.
- 1억 개의 합성 증명 데이터로 사전 훈련된 모델을 기반으로, 특정 작업에 더 잘 맞추기 위해 900만 개의 증명으로 미세 조정을 수행했음.
Why LM is needed ?⚑
- 상징적 추론 엔진(DD + AR)은 순수한 연역 단계로 문제를 해결하지만, 올림피아드 수준의 문제를 해결하기 위해서는 새로운 증명 용어를 생성하는 것이 필수적.
- 이러한 증명 단계는 상징적 추론 엔진이 설계되지 않은 보조 구성을 필요로 함.
- 이전 방법들은 수작업으로 제작된 템플릿과 도메인 특화 휴리스틱을 기반으로 했기 때문에, 하드코딩된 규칙에 의해 인간 경험의 일부만 다룰 수 있었음.
- 반면, 합성 데이터로 훈련된 신경 해결사는 인간의 시범 없이 처음부터 보조 구성을 수행하는 방법을 학습했음.
Example⚑
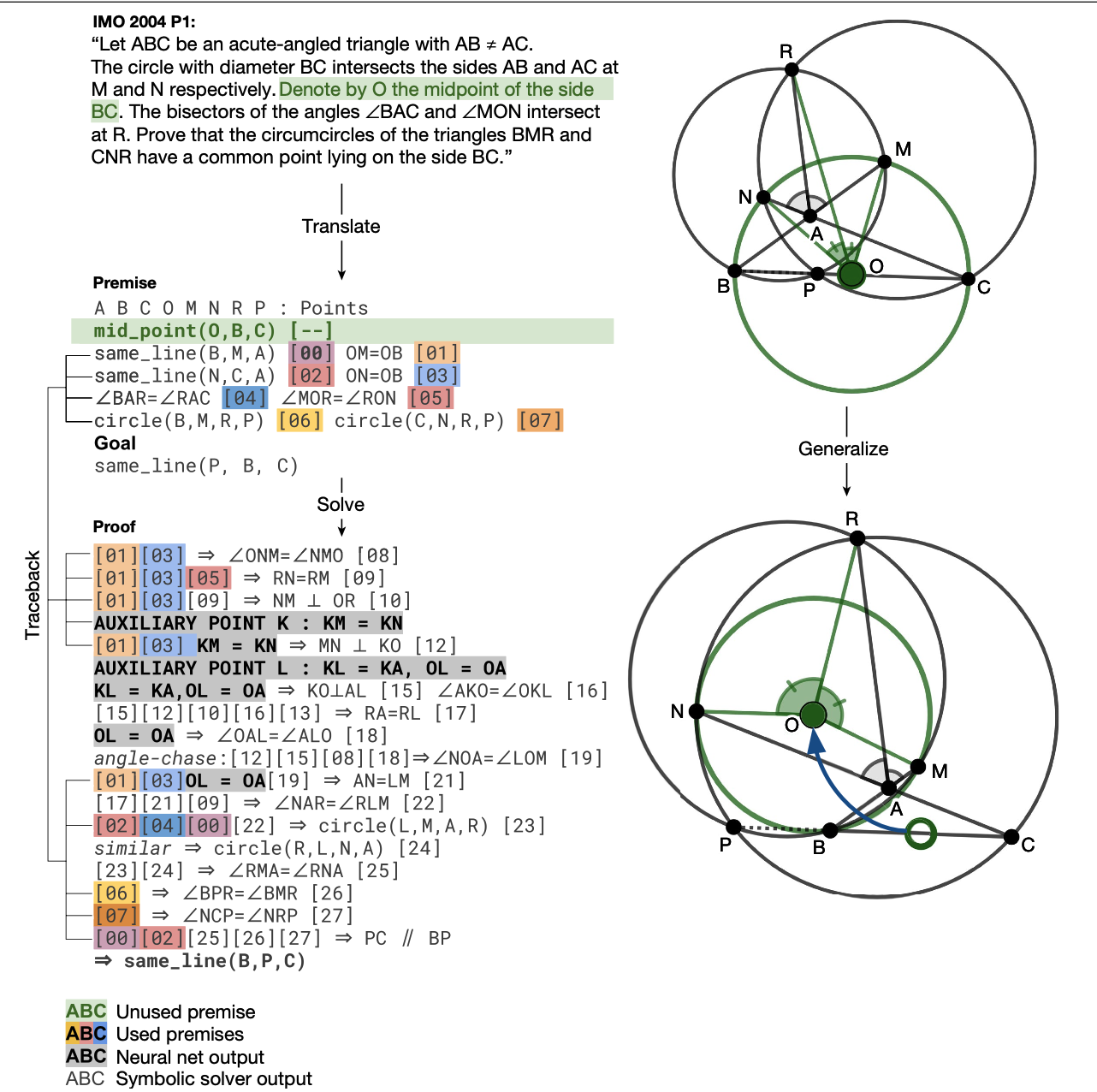
- 실제 예시에서 주어진 전제로부터 AlphaGeometry 는 새로운 보조점(회색)을 생성하고,
- 지속적으로 Deduction Engine 과 AR 을 통해서 증명을 생성하는 과정을 확인할 수 있다.