periodic-phenomenon

순환하는 것들에 대한 고찰⚑

• 세상에는 순환하는 현상이 가득하다.
• 이와 같은 현상을 수학적으로 설명하기 위한 방법 중 하나로 Lotka-Volterra 방정식이 있다.
• Lotka-Volterra 의 기본적인 아이디어는 두 주체 간 상호작용의 결과로서 주기적인 변동이 나타난다는 것이다.
• 사이클 그 자체를 하나의 현상으로 보기보다는, 무엇이 사이클을 만들어내는지에 주목하는 것이 중요하다.

Lotka-Volterra 방정식⚑

• 이 모델은 다음 두 개의 미분방정식으로 표현된다:

• \(\frac{dx}{dt} = \alpha x - \beta x y\)

• \(\frac{dy}{dt} = -\gamma y + \delta x y\)

• 각 변수와 파라미터는 다음을 의미한다:

  • \(x(t)\): 시간 \(t\)에서의 토끼 개체 수.
  • \(y(t)\): 시간 \(t\)에서의 여우 개체 수.
  • \(\alpha\): 토끼의 출산율.
  • \(\beta\): 여우에게 토끼가 잡아먹힐 확률.
  • \(\gamma\): 여우의 자연 사멸률.
  • \(\delta\): 여우가 토끼를 잡아먹음으로써 얻는 영양분.

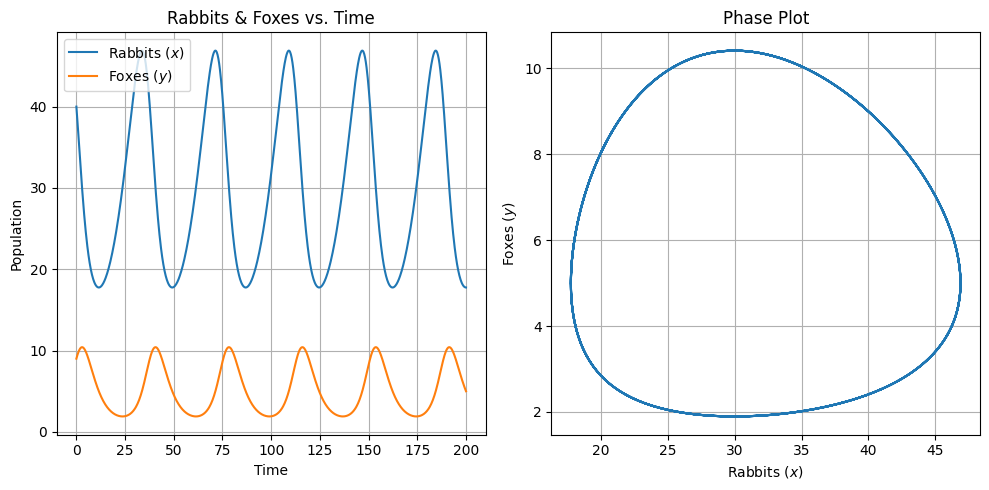
• Lotka-Volterra 방정식은 포식자와 피식자의 개체 수 변화를 수학적으로 설명한다.

• 요약하자면, 피식자의 숫자가 많아지면 포식자의 숫자도 증가하며, 포식자의 숫자가 많아지면 다시 피식자의 숫자가 감소하는 상호작용을 모델링한다.

순환현상의 설명⚑

• 이 방정식을 풀면 포식자와 피식자의 개체 수가 주기적으로 증감하는 패턴이 나타난다.
• 이는 자연에서 관찰되는 주기적 변동과 일치하며, 순환현상의 원인과 특징을 이해하는 데 기여한다.

경제학에서의 순환현상⚑

• 경제학에서도 비슷한 순환현상이 발견된다. 경제의 호황과 불황은 포식자-피식자 모델과 유사한 패턴을 보여준다.
• Lotka-Volterra 방정식을 바탕으로 경제 내 다양한 요소 간 상호작용을 해석할 수 있다.

경제 주체 간의 관계⚑

• 포식자와 피식자의 관계처럼, 경제 주체들 사이에서도 유사한 상호작용이 나타난다.

• 시장 공급자와 수요자의 관계

  • 피식자(수요)와 포식자(공급)로 해석 가능하다.
  • 수요가 증가하면 공급자도 증가하지만, 과잉 공급은 다시 공급자 감소로 이어진다.

• 경쟁 회사 간 상호작용

  • 두 회사가 시장에서 경쟁하며, 한 회사의 성장은 다른 회사의 점유율 감소를 초래한다.
  • 이런 역학은 Lotka-Volterra 방정식과 유사한 패턴을 보여준다.

• 금융 시장에서의 투자와 대출

  • 대출 금리와 투자 간의 관계도 포식자-피식자 모델로 해석할 수 있다.
  • 낮은 금리는 투자 증가를 유도하지만 과도한 대출은 경제적 부담을 초래해 투자를 감소시킬 수 있다.

Goodwin 모델⚑

• 경제에서의 주기적 현상을 설명하는 모델 중 하나이다.
• 노동과 자본 간의 상호작용을 바탕으로 임금과 고용의 흐름을 설명한다.

• Goodwin 모델은 다음 미분방정식으로 표현된다:

• \(\frac{dN}{dt} = rN - \phi(N)W\)

• \(\frac{dW}{dt} = -hW + \psi(N)W\)

• 각 변수는 다음을 의미한다:

  • \(N\): 고용률.
  • \(W\): 실질 임금.
  • \(r\): 인구 증가율.
  • \(\phi(N)\): 생산률 함수.
  • \(h\): 임금 증가율.
  • \(\psi(N)\): 임금 설정 함수.

• 핵심은 고용률과 임금 간의 상호작용이다. 고용률 상승은 임금 증가를 유발하고, 이는 다시 고용 감소로 이어질 수 있다.

마무리⚑

• Lotka-Volterra 방정식은 자연의 순환현상을 이해하는 중요한 도구다.
• 경제학에도 이를 응용함으로써 복잡한 현상을 분석하고 예측할 수 있는 통찰을 제공한다.
• 두 주체 간 상호작용에 따른 순환의 원리를 이해하는 데 기여한다.